Dado que existe un único
polinomio interpolador para un determinado conjunto de puntos, resulta algo confuso llamar a este polinomio el polinomio interpolador de Lagrange. Un nombre más conciso es interpolación polinómica en la forma de Lagrange.
En esta imagen se muestran, para cuatro puntos ((−9, 5), (−4, 2), (−1, −2), (7, 9)), la interpolation polinómica (cúbica) L(x), que es la suma de la bases polinómicas escaladas y0l0(x), y1l1(x), y2l2(x) y y3l3(x). La interpolación polinómica pasa exactamente por los cuatro puntos (llamados puntos de control) y cada base polinómica escalada pasa por su respectivo punto de control y se anula cuando x corresponde a los otros puntos de control.
Definición
Dado un conjunto de
k + 1 puntos

donde todos los
xj se asumen distintos, el
polinomio interpolador en la forma de Lagrange es la
combinación lineal

de bases polinómicas de Lagrange

Demostración
La función que estamos buscando es una
función polinómica L(
x) de grado
k con
El problema de interpolación puede tener tan solo una solución, pues la diferencia entre dos tales soluciones, sería otro polinomio de grado
k a lo sumo, con
k+1 ceros.
Por lo tanto,
L(
x) es el único polinomio interpolador.
Concepto
La resolución de un problema de interpolación lleva a un problema de
álgebra lineal en el cual se debe resolver un
sistema de ecuaciones. Usando una
base monómica estándar para nuestro polinomio interpolador, llegamos a la
matriz de Vandermonde. Eligiendo una base distinta, la base de Lagrange, llegamos a la forma más simple de
matriz identidad =
δi,j, que puede resolverse inmediatamente.
Uso
Ejemplo
Se desea interpolar
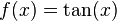
en los puntos
Con cinco puntos, el polinomio interpolador tendrá, como máximo, grado cuatro (es decir, la máxima potencia será cuatro), al igual que cada componente de la base polinómica.
La base polinómica es:





Así, el polinomio interpolador se obtiene simplemente como la combinación lineal entre los
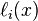
y los valores de las
abscisas:

-



Desventajas de su uso
Si se aumenta en número de puntos a interpolar (o nodos) con la intención de mejorar la aproximación a una función, también lo hace el grado del polinomio interpolador asi obtenido, por norma general. De este modo, aumenta la dificultad en el cálculo, haciéndolo poco operativo manualmente a partir del grado 4, dado que no existen métodos directos de resolución de ecuaciones de grado 4, salvo que se puedan tratar como ecuaciones bicuadradas, situación extremadamente rara.
La tecnología actual permite manejar polinomios de grados superiores sin grandes problemas, a costa de un elevado consumo de tiempo de computación. Pero, a medida que crece el grado, mayores son las oscilaciones entre puntos consecutivos o nodos. Se podría decir que a partir del grado 6 las oscilaciones son tal que el método deja de ser válido, aunque no para todos los casos.
Sin embargo, pocos estudios requieren la interpolación de tan sólo 6 puntos. Se suelen contar por decenas e incluso centenas. En estos casos, el grado de este polimonio sería tan alto que seria inoperable. Por lo tanto, en estos casos, se recurre a otra técnica de interpolación, como por ejemplo a la
Interpolación polinómica de Hermite o a los
splines cúbicos
Otra gran desventaja, respecto a otros métodos de interpolación, es la necesidad de recalcular todo el polinomio si se varía el número de nodos.
Otras aplicaciones
Aunque el polinomio interpolador de Lagrange se emplea mayormente para interpolar funciones e implementar esto fácilmente en una computadora, también tiene otras aplicaciones en el campo del álgebra exacta, lo que ha hecho más célebre a este polinomio, por ejemplo en el campo de los proyectores ortogonales:
Siendo I la matriz identidad.
Demostración:
Haciendo uso de la descomponsición espectral y aplicando las propiedades de los proyectores:

























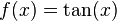 en los puntos
en los puntos
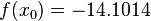



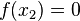
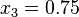
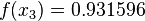
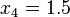






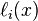 y los valores de las
y los valores de las 



 . Donde
. Donde  son los proyectores ortogonales y
son los proyectores ortogonales y  los autovectores de F asociados a cada proyector. Entonces:
los autovectores de F asociados a cada proyector. Entonces:
